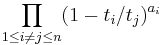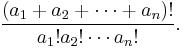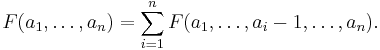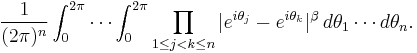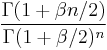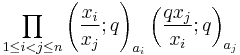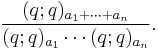Dyson conjecture

In mathematics, the Dyson conjecture (Freeman Dyson 1962) is a conjecture about the constant term of certain Laurent polynomials, proved by Wilson and Gunson. Andrews generalized it to the q-Dyson conjecture, proved by Zeilberger and Bressoud and sometimes called the Zeilberger–Bressoud theorem. Macdonald generalized it further to more general root systems with the Macdonald constant term conjecture, proved by Cherednik.

Contents

Dyson conjecture

The Dyson conjecture states that the Laurent polynomial

\prod _{1\le i\ne j\le n}(1-t_i/t_j)^{a_i}

has constant term

\frac{(a_1%2Ba_2%2B\cdots%2Ba_n)!}{a_1!a_2!\cdots a_n!}.

The conjecture was first proved independently by Wilson (1962) and Gunson (1962). Good (1970) later found a short proof, by observing that the Laurent polynomials, and therefore their constant terms, satisfy the recursion relations

F(a_1,\dots,a_n) = \sum_{i=1}^nF(a_1,\dots,a_i-1,\dots,a_n).

The case n = 3 of Dyson's conjecture follows from the Dixon identity.

Sills & Zeiberger (2006) and (Sills 2006) used a computer to find expressions for non-constant coefficients of Dyson's Laurent polynomial.

Dyson integral

When all the values ai are equal to β/2, the constant term in Dyson's conjecture is the value of Dyson's integral

\frac{1}{(2\pi)^n}\int_0^{2\pi}\cdots\int_0^{2\pi}\prod_{1\le j<k\le n}|e^{i\theta_j}-e^{i\theta_k}|^\beta \, d\theta_1\cdots d\theta_n.

Dyson's integral is a special case of Selberg's integral after a change of variable and has value

\frac{\Gamma(1%2B\beta n/2)}{\Gamma(1%2B\beta/2)^n}

which gives another proof of Dyson's conjecture in this special case.

q-Dyson conjecture

Andrews (1975) found a q-analog of Dyson's conjecture, stating that the constant term of

\prod_{1\le i<j\le n}\left(\frac{x_i}{x_j};q\right)_{a_i}\left(\frac{qx_j}{x_i};q\right)_{a_j}

is

\frac{(q;q)_{a_1%2B\cdots%2Ba_n}}{(q;q)_{a_1}\cdots(q;q)_{a_n}}.

Here (a;q)n is the q-Pochhammer symbol. This conjecture reduces to Dyson's conjecture for q=1, and was proved by Zeilberger & Bressoud (1985).

Macdonald conjectures

Macdonald (1982) extended the conjecture to arbitrary finite or affine root systems, with Dyson's original conjecture corresponding to the case of the An−1 root system and Andrews's conjecture corresponding to the affine An−1 root system. Macdonald reformulated these conjectures as conjectures about the norms of Macdonald polynomials. Macdonald's conjectures were proved by (Cherednik 1995) using doubly affine Hecke algebras.

Macdonald's form of Dyson's conjecture for root systems of type BC is closely related to Selberg's integral.

References